Sammanfattning: Kan en förenklad formel användas för att beräkna hcp-justeringar i bridge? Kan den enkla formeln DHcp = (50-HPct)/F, där F är en faktor som beräknas och är en funktion av antalet spelade brickor och par som deltar i tävlingen i storleksordning 10-20.
Svaret är ja, med vissa reservationer.
Är bridge prestige och prestation? Nä mest ett intressant och stimulerande fritidsintresse…
Det finns dock några jag känner (mig själv åtminstone), som tycker det är intressant att kunna följa de försök man gör för att bli bättre, ”handikapp-jägarna” kallade. Vi kom in för sent för att kunna delta i mästarpoäng-racet och får då hålla tillgodo med hcp.

För att tillgodose denna grupp och samtidigt försöka få bridgen mer intressant för flera, så fanns en förebild i golfen, som med sitt hcp-system lyckats bredda intresset. 2005 publicerade förbundet en skrift som blev avstampet till ett generellt hcp-system för bridge i Sverige, som skulle ersätta alla hittills hemmagjorda system.
Första gången jag läste detta dokument blev jag förbluffad/förvånad… Sen kom tanken: ”Hur svårt kan det vara?”
Jag har arbetat i hela mitt yrkesverksamma liv med att försöka hjälpa människor att tolka siffror, så de kan omsätta fakta de följer på ett konstruktivt sätt. Detta dokument var: ”Hur kan jag med formler skapa siffror som ingen begriper.” Det fanns säkert riktlinjer och tankar då 2005 som präglade detta dokument och efter att ha tjänat oss i bridgevärlden i femton år som inspirations-källa för att mäta om vi blivit bättre kan det vara dags för en revision på de erfarenheter som gjorts och den implementation som förverkligats. Så har jag tänkt en tid….
Ett axplock av formler för att belysa mina tankar runt mystiken. Formeln för att räkna ut hur min prestation på en tävling påverkar min hcp är den mest spännande:
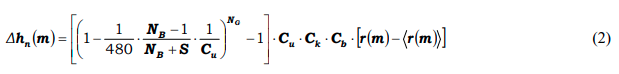
Där det det ingår storheter som antalet bord, antalet spelade brickor och diverse utspädningsfaktorer som är framräknade med statistisk signifikans… I mina yngre dagar vid universitet lärde jag mig tolka slika formler, så jag har sett värre odjur i kvantmekaniken min dagar…
Vidhåller dock fortfarande att de vackraste formlerna är de enkla:

Vidare om hcp då, för att beräkna uttrycket till höger ska följande formel användas:
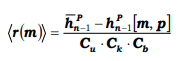
Man kan gräva djupare och hittar då följande formel:
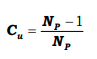
Någonstans 2005 missade man något mot det golfen begripit. Fick jag 36p på rundan gick jag på min hcp, över var bra under var dåligt! Sen fanns en tabell jag kunde slå upp hur mycket mitt hcp påverkades direkt efter en runda.
HCP-systemet måste vara begripligt för att nå acceptans! Gärna också direkt omsättningsbart i direkt koppling till prestationen. Det senare har SBF anammat nu då man efter en tävling kan få ett approximativt värde på hur hcp:n påverkas direkt efter en tävling. Detta har gjorts genom att man inför två begrepp spelhcp och livehcp. Kanske inte enklare men mer direkt beräknat efter spelad tävling.
Egentligen är ju det hela väldigt enkelt, tittar jag på mitt hcp-resultat så vet jag att 50% är som 36p i golf, dvs som förväntat. Allt över är bra och innebär en sänkning och allt under är dåligt och innebär en höjning av min hcp. Frågan är då bara hur mycket? Man kan ju tycka att var det många deltagare eller många brickor så borde resultatet påverka lite mer än på en vanlig tävling på klubben. Sen kan man ju tycka att ett dåligt resultat inte direkt ska sänka mig till resultatet av den senaste prestationen, men fortsätter det på samma sätt i 15-20 tävlingar får jag acceptera att jag blivit så mycket sämre eller bättre. Det känns på något sätt rimligt att min avvikelse för en viss tävling divideras med något tal mellan 10-20… Dvs en formel enligt: HcpNy = HcpFg + (HPct – 50)/F , där F är mellan 10 och 20.
Om vi antar att för ett visst antal deltagare och spelade brickor är F=10 och du presterar 54,5% som hcp-resultat, formeln innebär då att om din hcp är 31,50 så sänker du dig med 4,5/10 = 0,5 så du får ny hcp = 31,00.
I grunden är det detta enkla samband som formlerna från 2005 försöker uttrycka! Kan man då med en så enkel formel åstadkomma samma sak som de omfattande formlerna i förbundets datorer? Kanske inte på hundradelen, men vad har det för betydelse? Viktigt är att hcp i bridge är ett nollsumme spel? Dvs i en tävling sker lika mycket höjningar som sänkningar? Eller kanske det skulle födas lite hcp-poäng för de som är flitiga? Hur som helst inte ens det nuvarande systemet är noll-summa då spel i ett gäng med många 52-hcp som ska höjas sänker gruppens hcp med automatik och därmed delas det ut gratis hcp-poäng i sådana gäng – ”ankdamms-effekten”.
Vad är då F? De parametrar som styr formlerna för justering är:
THcp Tävlingens handikapp, dvs medelvärdet för alla deltagande spelare
NG Antalet spelade givar
NP Antalet par som deltagit i tävlingen
NB Antalet bord som tävlingen omfattade
Sen finns ett antal konstanter som beräknats på statistiska grunder.
Om formlerna i dokumentet är de som verkligen används i SBF:s beräkningar är inget jag kunnat fastställa, utan det är ett antagande jag gjort, som jag tyckte rimligt…
Vi provar att fastställa F empiriskt, dvs vi tittar på en person (ego 29718) och utvecklingen av hcp som finns på BIT:
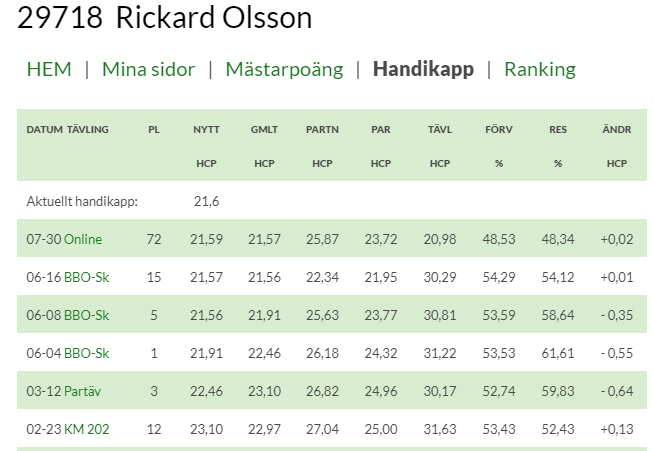
Kopierar ned datat till Excel och tar bort en del tävlingar som inte är enhetliga. Jag spelar normalt i tre olika tävlingar: Tisdagar i Lomma (11), Onsdag ibland i Bjärred(5) och torsdagar i Bjärred någon gång i Lomma (13) – alla med olika partners.
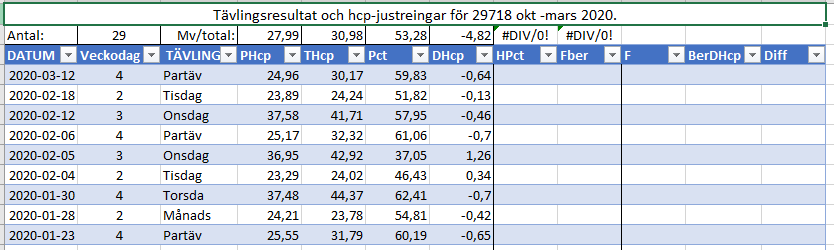
Första uppgiften är att försöka bestämma F för de olika tävlingarna, oftast är det samma par och samma antal brickor som spelas, så ett medelvärde över de olika tävlingarna borde vara ett bra startvärde på F för den givna tävlingen. Vi börjar med att beräkna HPct, dvs handikapp-resultatet med formeln: HPct = Pct + (PHcp-THcp)/2, där HPct = Resultat omräknat efter hcp, Pct = scratch-resultat, PHcp = parets hcp och THcp är medelvärdet på hcp för deltagarna i tävlingen.
Då vi har facit på DHcp (sänkningen av hcp), som vi vill beräkna med formeln BerDHcp = (50-HPct)/F, får vi att F kan beräknas med formeln FBer = (50-HPct)/DHcp vilket är den formel vi använder, F sätter vi sedan till medelvärdet för den angivna tävlingstypen och beräknar sedan BerDHcp och diffen mot facit:
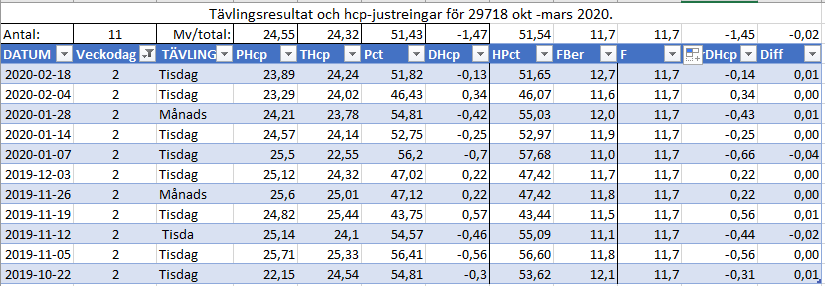

Torsdagarna ställer till det lite, F vissa dagar runt 10 andra runt 12? Avvikarna är Lomma med färre brickor liksom avslutning i Bjärred (inget som syns – men jag vet att hög THcp är Lomma))
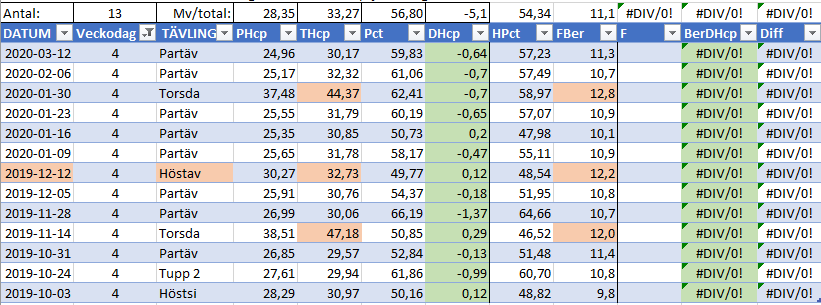
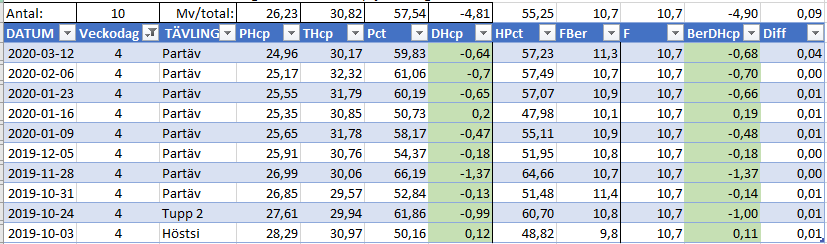
Modellen är färdigbyggd återstår att se hur bra den blev:

En graf som belyser modellens effektivitet: (blått är facit, brunt är modellen)
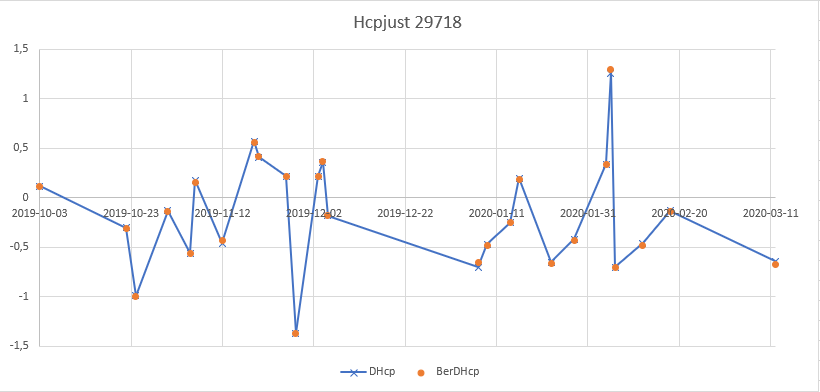
Så då återstår att fastställa är värdena för F bara beroende av NP (antalet deltagande par) och NG (antalet spelade givar). Låt oss försöka beräkna NP och NG för tävlingarna ovan som en första ansats. Vi tar med några fler spelae och spel från olika lokaler.
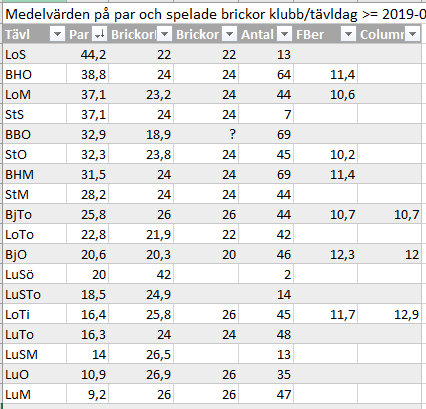
Så frågan man kan ställa sig är ju hur känslig är beräkningen ifall F-värdet är felaktigt, dvs en känslighetsanalys. Det verkar inte helt oväntat som osäkerheten för bestämning av en korrekt justering över flera tävlingar beror på om det är en stor eller mindre justering samt antalet tävlingar som ingår Dvs vid stor hcp-förändringar över ett fåtal tävlingar blir beräkningen betydligt känsligare för felbestämda F-värden.

Här redovisas en hcp-förändring som enligt facit är -4,53, om F är felbestämt +/-0,5 enheter får vi -4,38 eller -4,82 som estimat. Om vi ökar felet i F till 1,0 blir motsvarande intervall: -4,19 och -5,08 dvs osäkerheten är 0,5 hcp-enheter. Ökar vi F-felet till 2 enheter blir intervallet -3,85 och -5,67 vilket nästan är en hcp-enhets osäkerhet. Dvs modellen verkar vara tillräckligt stabil även om framräknade F är behäftade med måttliga fel. Är hcp-justering mindre och antalet tävlingar som ingår fler blir känsligheten mycket mindre.

I ovanstående exempel (87540) där det finns ett underlag på 38 tävlingar och den korrekta justeringen är +0,25 så estimeras justeringen till 0,22 hcp-enhet, dvs modellen är nästa helt okänslig för felbestämds F-värden i denna situation. Fler exempel redovisas i det bifogade Excel-arket.