Slutsatser:
Antalet hp som krävs för 50% chans att kontraktet ska gå hem med DD-spel:
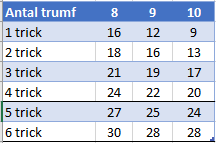
Baserat på verkligt spel av par med hcp<36 kan man få fram följande tabell där utfallet i snitt är över 50%:
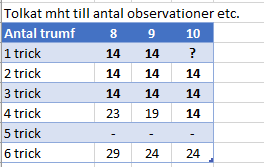
Dra inte slutsatsen som i den andra tabellen att hp-gränserna är riktvärden, utan här ska de tolkas som att skickliga spelare gör tilläggsvärderingar som gör att de ibland bjuder högt och lönsamt med låga hp-värden!
Undersöker man zonberoenden finner man att det är inte lönsamt att bjuda i zonen på 3-tricks nivån med 8 trumf, däremot ok i Ozon. I övrigt verkar angivna gränser innebära lönsamma kontrakt, dock troligen måste nog hänsyn tas till andra faktorer än trumflängd och hp. Vilka?
Vill du veta bakgrunden får du gärna fortsätta läsa.
I grundkursen lär vi oss att bjuda 4 med 25hp och lillslam med 33. Med lite rutin i partävlingar tummar vi en del på dessa konservativa regler anpassade för robberbridge och lagtävling. Detta är då baserat på att utgång/slam ska bjudas om sannolikheten att det går hem är 50% eller mer. Förr fick man också lära sig att räkna fp och stp, vilket då ger något bättre rådgivning för lite obalanserade händer. Men i grundkursen ges ingen vägledning hur högt man ska bjuda i konkurrenssituationer, vilka oftast uppstår med 18-22hp (ca 40% av givarna) och att motståndarna hittar en färg, vilket de oftast har om vi själva har en 8-korts högfärg.
I Moderns Standard är ofta fp och stp borttagna och man ombedes i stället att räkna med + och – för färglängd, anpassning, vilka färger man har höga kort, sekvenser eller gafflar osv, med rådet har du många plus var optimist med många minus bromsa! Vidare lär man ofta ut att poängregler är bara en vägledning, hur många stick man kan ta beror på många andra faktorer än hp. Detta är ju i sig sant, men jag har alltid önskat lite mer vägledning… Tyvärr är de flesta böcker skriva av bridge-rävar med stor erfarenhet av lagtävlingar, vilket gör att så lite ansträngningar görs för de ”tråkiga” delkontrakts-brickorna som dessvärre ofta är avgörande i partävlingar.
Det påstås ofta i bridgelitteraturen att det i teorin är lönsamt att bjuda utgång i högfärg när chansen att den går att spela hem är 50% eller högre… Men hur vet man det ? När man får upp träkarlen kan man i vissa fall göra en uppskattning på sannolikheten att utgången går att spela hem, men ganska svår beräkning även i detta läge. Hur ska man då kunna göra den bedömningen strax innan i budgivningen. Erfarenhet… Men om man inte har det hur gör man då?
Är 50% rätt mer än teoretiskt? Är det rätt teoretiskt? Om vi antar att alla par antingen bjuder 3hj eller 4hj, vilket i sig är en kraftig förenkling av verkligheten. Dessutom spelar alla lika och tar lika många stick. Dvs beroende på hur många som är i respektive grupp antar vi att vi får q% om vi bjudit 4hj och spelar hem det, vi får då 1-q% om det är en bet. Vidare antar vi att sannolikheten att vi spelar hem kontraktet 4hj är p, då är sannolikheten att vi går en bet 1-p. Dvs vi får då följande samband:
Vårt utfall blir då: p*q + (1-p)*(1-q) = 1 – p – q + 2pq > 0,5 vilket ger (p-0,5)*(q-0,5) > 0
Om vi utgår från att q > 0,5, dvs vi får mer än 50% om vi spelar hem 4hj. Vi inser då att det krävs p > 0,5!!
Dvs med denna förenkling dyker 50% upp! Med de mer komplexa förhållande som gäller i verkligheten, ett par tar en ÖT och två par får en bet, ett par spelar 3hj+1 etc.. Då blir det hela genast mer komplext, så låt oss konstatera 50% är möjligtvis en riktsiffra för partävling och mest korrekt för lagtävling, men även här finns avvikelser beroende på zonerna att ta hänsyn till. Låt oss ändå börja med den. Ett sätt att få grepp om dessa svårfångade 50% kan ju vara att omsätta det till kunskap man uppsnappar under budgivningen, dvs gemensamt antal hp och den trumflängd man förfogar över. Ok i de flesta lägen har vi kanske inte exakta tal på dessa storheter utan måste nöja oss med intervall-skattningar. Men ofta vet vi exempelvis: minst 9-korts trumf och 23-24 hp tillsammans… Kan då denna kunskap omsättas till en sannolikhet?
Vi börjar med att gå igenom de brickor som finns lagrade och är hämtade från PBN-filer i Spader/BIT (119 631), av dessa är ett antal bortvalda dels då kortgivarna saknas dels då de har någon misstänkt allvarlig felregistrering. Troligtvis är en del giltiga bortvalda samtidigt som det finns en del med felregistreringar som återstår totalt har vi då 110 946 med det dubbla antalet parvis samsade händer drygt 220′. Vi hittar 84 215 brickor där något par förfogar över en 8-korts högfärg eller längre, dvs 84215/221892 = 38% av brickorna. Totala antalet parvisa är dock 108139/221892 = 49%, dvs det händer inte så sällan (11%) att man har varsin högfärg.
Läser vi av DD-tabellen i BIT/Spader ser vi hur många stick som finns för respektive väderstreck dels i trumfspel dels i NT.
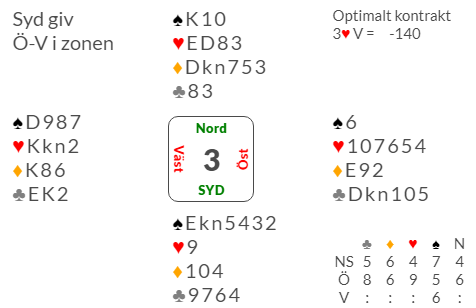
I exemplet ovan har NS 8sp och 17hp och ÖV 8hj och 23hp. Hur högt ska de bjuda? ÖV kan spela hem 9 stick med hj som trumf medan NS bara har 7 stick med spader som trumf. En av många möjliga budgivningar kunde vara:
p-1NT-p-2ru-p-2hj eventuellt med tillägget p-2NT-p-4hj om Öst är överoptimistisk.
Öst har en trevlig klöver men 5 hackor i trumf är en varningssignal, när Öst tar sitt beslut överblickar hen 22-24 hp och minst 7hj. Bästa budet i långa loppet är nog pass. En annan Öst tycker klöverfärgen är fin och bjuder 2NT. Nu är det då Väst som beslutar, ser 8hj och 24-25hp. Detta är ju en indikation på att 4hj är en spelbar utgång… När Väst ser bordet blir ju bedömningen lätt att det är 75% chans att kontraktet går att spela hem om bara inte N har ED i hj, men även då borde det kunna gå. N kan spela ut allt utom hjD för att det ska bli bet. Naturligt är väl kl8 som Öst tar. Om V sedan rör trumfen finns risk för två bet… Allt analyserat med DD-solver:
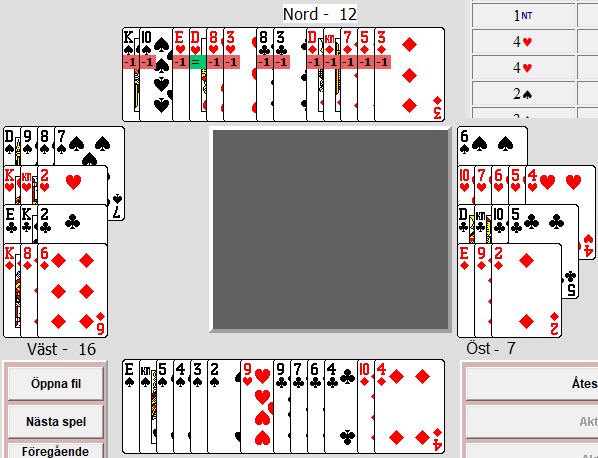
Ingen lyckades ta 10 stick utan de flesta har landat på exakt 9, vilket var det som stod i DD-tabellen. Det är oftast så att tabellen ger en bra bild över hur många stick man kan få.
Så låt oss titta på vad en genomsökning av databasens alla brickor ger där någon sida har 8-korts högfärg och samtidigt läsa av hur många hp de förfogar över. Därefter låter vi datorn titta i DD-tabellen och se efter hur många stick som finns. Vi samlar upp resultatet i ett Excel-kalkylark så vi kan analysera siffrorna enkelt:
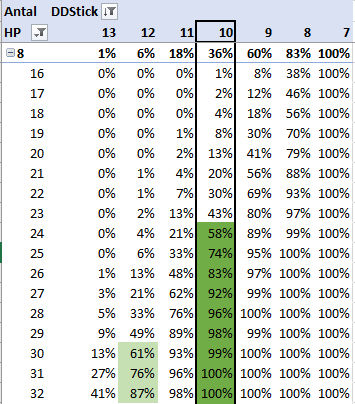
I tabellen visas om man har 8 trumf möjliga DD-stick överst och i första kolumnen anges gemensamma antalet hp från 16-32. Siffran anger hur stor andel av brickorna med där man kan lyckas spela hem och är alltså en skattning av de där 50% man är ute efter. Man kan läsa av att 4hj/sp är hemma 58% av fallen om man har 24hp med det bara är 43% chans med 23hp. Man kan också se att lillslam bör prövas med 30hp tillsammans och 8-korts trumf. Dvs om det nu är 50% chans som är det riktiga värdet i en MP-tävling…

Tittar man vidare i tabellen kan man göra följande sammanställning:
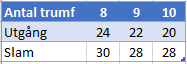
Denna tabell visar när chansen att kontraktet ska gå hem är mer än 50%! Men visst det finns andra faktorer att ta hänsyn till också… Som en vägledning är den användbar. Tilläggas ska att när det gäller slam är det 49% chans till framgång med 27hp och 10 trumf liksom med 29hp och 8 trumf. OBS! Detta är teoretiska siffror framtagna utan hänsyn till verkligt spel.
Man kan också göra en annan analys med databasen där man i stället ser efter hur utfallet varit för de som bjudit ett visst kontakt med en viss trumflängd och ett visst antal hp. Detta blir ju en test av verkliga livet. I denna undersökning kan det finnas skäl att exkludera resultat från mindre rutinerade spelar så i denna utsökning ingår bara givar där båda paren minst har <= 36, vilket motsvarar c:a 40% av de som spelar bridge i klubbsammanhang.
I den vänstra delen tabellen nedan visas utfall i % i medeltal som för de som bjudit olika nivåer på HF-kontrakt med 8 trumf och olika antal hp.
OBS! Endast resultat från brickor där båda paren har en hcp understigande 36.
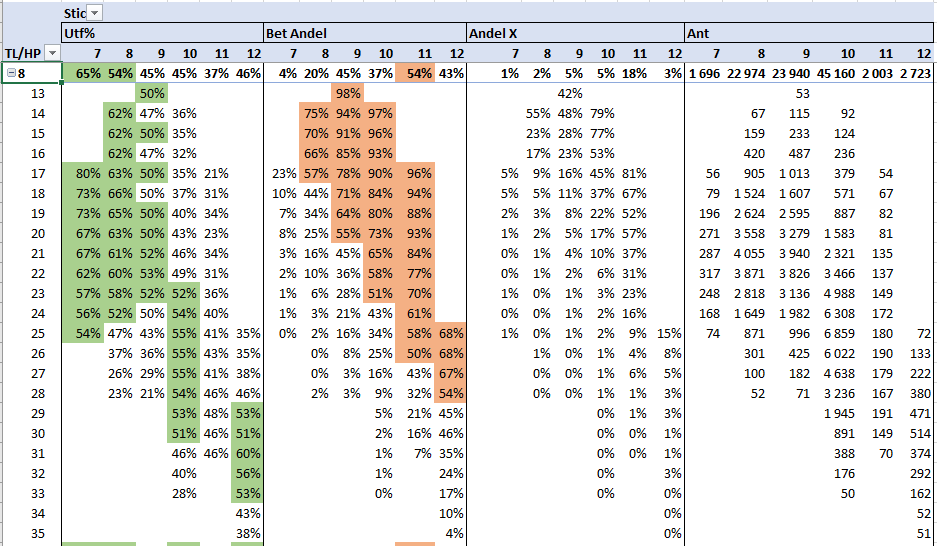
Vi börjar med kontraktet 1hj/sp (7 stick) och ser att det oftast är dyrt att släppa motståndarna så billigt, utfallet är 54-80% med 65% i medel, ju mindre hp de har desto mer lönsamt! I tabellens högra del visas hur många resultat som hittats, en godtycklig gräns på 50 observationer är satt för att undvika felaktiga data. Underlaget för 1HF är med andra ord ganska magert.
Även 2hj/sp är lönsamma kontrakt 54% i medelutdelning. Blir bara dåligt utfall när de missat en utgång med 25hp+.
3hj/sp är ett svårbedömt kontrakt med runt 50% oberoende av om man har 13-24hp. Vi får nog anta att den spelargrupp vi tittar på använder andra kriterier än bara uppskattad trumflängd och hp-styrka. Dvs de bjuder 3HF på ”rätt” händer… Om man tittar på betfrekvens ser man att 3sp är bet i mer än 50% av fallen om man har under 21hp. Att utfallet blir bra för sådana offringar beror till stor del på att risken att bli dubblad i 3HF är relativt låg (5% totalt) med ökande risk när antalet hp tryter.
4hj/sp är lönsamt för de som bjuder det med 23-30hp och åtta trumf. DD-analysen gav siffrorna 24-29, vilket ju är en överraskande bra överensstämmelse!
5hj/sp verkar vara det sämsta kontraktet att bjuda, snittar aldrig över 50% ens för så duktiga spelare som vi tittar på här. Det är ett svårbedömt läge och rådet som står i litteraturen stämmer väl – ”five never”! Har förstås också att göra med att det är det kontrakt som dubblas oftast 18% av fallen! Det går oftast bet om man inte har 26hp+.
6hj/sp lillslam i HF är kanske mer lönsam än sitt rykte, de flesta väljer ju 6NT när antalet hp tycks räcka. Tabellen säger har man mellan 29-33hp är det lönsamt i längden. För 33hp är underlaget relativt mager och för högre hp-styrka är det troligen så att de flesta valt att spel i NT.
Det finns i Excel-arket även framtagit siffror för när man har 9,10 och 11 trumf. Av naturliga skäl sjunker behovet av honnörer när trumfen ökar i längd. Sammanställer vi i en tabell får vi följande riktlinjer baserat på utfall >= 50% i medeltal.
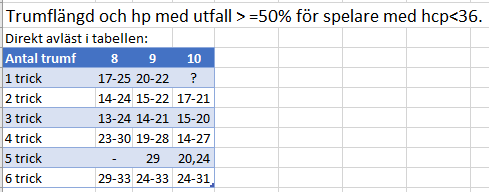
Direkt avläsning i tabellen ger lite ologiska intervall då det i vissa rutor saknas ( mindre än 50 observationer) underlag. Med 9-kort trumf är det ju ovanligt att man får spela på 1 trick exempelvis. Nedan har gjorts ett försök till lite mer logisk tolkning av resultatet:

Dvs bjud upp till 3 trick om ni har 14hp+ med 8 eller 9 trumf. Med 10 bjud 4 alltid! Vi ser också att det kan vara lönsamt att bjuda högre än DD-analysen gav vid handen, då det ju i verkliga livet ibland är lönsamt att göra en offring, speciellt där dubblings-risken är låg.
OBS! Tabellen får inte tolkas som att alla kombinationer med 14hp är lönsamma att bjuda 2/3HF med! Det är ju så att dessa händer är bjudna av levande människor (hcp<36) vilket gör att de har vägt in andra faktorer än bara hp. Att utdelningen på offringar är bra hänger samman med att dubblingsrisken är väldigt låg upp till 3 trick. Och det gäller som vanligt att göra offringarna vid rätt tillfälle beroende på zoner, tilläggsvärden och om motståndarnas kontrakt har stor chans att gå hem. Dvs helt andra aspekter än bara den egna hp-styrkan ska vägas in!
Man frapperas ändå av att ”lagen”-rådet som finns i alla moderna bridgeböcker verkar hålla i praktiskt spel. Dvs bjud 2 med 8 trumf, 3 med 9 och 4 med 10, och bjud direkt till den nivån om motståndarna går in! Antingen går kontraktet hem eller så blir det oftast en odubblad och därmed lönsam offring! Sen kan man med rätt tilläggsvärden gå lite lägre i hp-styrka än vad DD-tabellen anger. Att slammar på 24hp är lönsamma hänger ju i stor utsträckning på om de bjuds så finns anpassning och bra tilläggsvärden samt att så få bjuder slam då, dvs utdelning blir mycket bra vid hemgång!
Hänsyn till zoner.
Offringar i zonen på delkontraktsnivå innebär alltid en risk för 2 bet -200 och en garanterat dålig bricka. Så frågan som inställer sig är ju, hur beror gränserna av zonförhållanden. Antalet rutor som blir tomma då det saknas 50 observationer blir ju då betydligt fler, så man få försöka tolka siffrorna med logik och fantasi. Detaljerna finns i Excel-arket. Det man kan se att det blir mindre lönsamt att bjuda på 3-trick med 8-kortsfärg i zonen och bör undvikas helt. 2- och 4-tricksnivån tycks vara mindre zonberoende. Med 9- och 10-kortfärg tycks ingen zon-anpassning behövas.