Budgivningen i bridge går ut på att försöka hitta hur många stick man kan få när man ser hälften av de 26 kort som man förfogar över. De egna resurserna är alltså till 50% kända när man plockat upp och sorterat sina 13 kort. Men inte ens med fullständig kunskap om de gemensamma resurserna kan man förutsäga hur många stick man kan få, då utfallet också är beroende av hur de okända 26 korten sitter, som finns hos motståndarna. För att utröna detta har man 38 budlappar i en låda till sitt förfogande som får väljas enligt speciella regler. Antalet möjliga kombinationer av alla möjliga budgivningar är mycket stort (1,29 E+47), så det verkar ju finnas möjlighet att med detta kodifierade språk kunna ta reda på det mesta om den egna sidans resurser och sedan genom att lyssna på motståndarna få reda på hur deras kort sitter….
För att hantera detta har olika “språk” utvecklats så att man kan kommunicera med budlapparna för utbyte av information, så kallade budgivningssystem och konventioner. Dessa är under ständig utveckling, men de flesta har vissa gemensamma nämnare: hitta styrkan i de gemensamma höga korten och att hitta en bra trumf om en sådan finns. Detta innebär att de flesta budlapparna man väljer ger information om hur många kort man förfogar över i en färg och hur många poäng som finns i de höga korten. Dvs de flesta systemen går ut på att hitta summan av hp/fp och om man har en gemensam färg med åtta kort eller fler som kan vara lämplig som trumf. Detta ska sedan kombineras med den trickiga poängberäkningen i bridge så man får ut maximalt antal poäng till den egna sidan i aktuell giv.
Detta innebär att man ska fatta beslut om antalet stick man vill spela om med de två parametrarna: summan av hp och den bästa färgens längd. Med trickiga konventioner kan man sedan ta reda på antalet ess, kungar man förfogar över liksom andra parametrar som om man har två gemensamma färger och om den hand som har minst antal kort i trumf har en kort färg vid sidan av etc etc, allt beroende på vart man är på väg.
Att använda HP för att bedöma möjligheten att ta stick stämmer ganska väl om man spelar NT med två relativt jämna händer – vilket inträffar i nästan var fjärde giv. Chansen att du får en balanserad hand är nästan 50% (10,5+21,5+15,5 = 47,5). De flesta sticken i NT tas med de höga korten vilket gör att HP-modellen i dessa fall ganska väl återspeglar hur många stick respektive sidan kan få. Variationen beror i NT mest på hur de höga korten sedan är fördelade mellan de olika händerna. Man lär sig som nybörjare att om man har 25hp och två balanserade händer ska man bjuda 3NT, vilket med denna kunskap ger c:a 50% möjlighet att spela hem de 9 sticken. De s.k. mellankorten (10,9) har större betydelse i NT än i färgspel men ger inga HP.
Om man spelar med trumf tillkommer möjligheten att ta stick med trumfen, vilket gör att betydelsen av de höga korten (speciellt D och kn) minskar och hur många trumf man förfogar över blir en allt viktigare faktor ju ojämnare fördelningen är mellan händerna. För att kunna utnyttja trumfen maximalt krävs dock att man är kort i en färg där partnern har längd, annars uteblir stöldsticken. Den bakomliggande poängberäkningen i bridge gör också att resurser i högfärgerna (sp/hj) är mer värdefulla än i lågfärgerna (ru/kl).
Av dessa skäl har mina analyser hittills bara varit baserade på den gemensamma styrkan i HP och längden på den längsta gemensamma färgen (BL) då denna information är den som framkommer i budgivningen, typ någonstans måste man ju börja.
Man kan betrakta antalet stick som är möjliga att ta som en funktion S av HP och BL, dvs matematiskt S(HP,BL). Hur ser då denna funktion ut? I en viss giv vet man naturligtvis inte detta förrän efter att given är spelad och värdet på S beror också på ett stort antal andra parametrar som spelskicklighet, fördelningar, var korten sitter etc etc, så man kan fråga sig hur tillförlitligt man kan förutsäga S i en given situation om man känner till HP och BL exakt, vilken man dessutom inte gör. Inte speciellt bra! Det är därför bridge är ett spel med stor variation. När väl S är känt kan man sedan fastställa funktionen P, dvs antalet poäng man tilldelas i den spelade brickan, där P är en funktion av kontraktet och antalet stick man skrapade ihop, dvs P(K,S). Spelar man sedan en partävling får man matchpoints (MP) som är beroende av hur andra har lyckats med exakt samma kort, dvs MP(P1,P2,….P15). Att vinna en bridgetävling är att få fler MP än motståndarna! Sambanden är komplexa minst sagt och låter sig inte formuleras i en enkel matematisk formel.
För att utröna ”bästa slutkontrakt” som en funktion av HP och BL har jag provat två metoder, dels att bland de givar som finns i databasen göra en DD-analys där antalet möjliga stick framräknas om man spelar på bästa sätt och vet exakt hur alla kort sitter dvs en mycket idealiserad bild av den som gäller vid spelbordet. Många tvivlar på om modellen ens är användbar. Som med alla förenklingar av verkligheten måste resultat från en sådan modell betraktas med skepsis, och undersökningar göras om de predikterade resultaten är tillförlitliga, mer finns att läsa här.
För att verifiera modellens validitet har jag provat ett annat sätt som anknyter direkt till utfallet i %, och MP. Jag har där använt alla registrerade resultat på spelade brickor och räknat fram medelvärdet på utfallet i % som funktion av Kontraktet, HP och BL. Modellerna är snarlika och försöker skapa underlag för hur högt man ska bjuda om man känner till HP och BL för den egna sidan. Sätter vi upp de två tabellerna vid sidan om varandra
| DD-analys Färgspel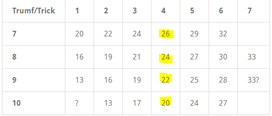 
NT |
Spelade brickor |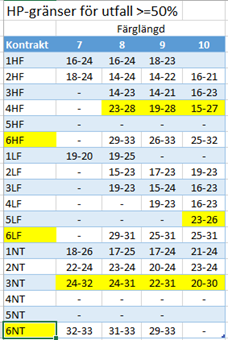
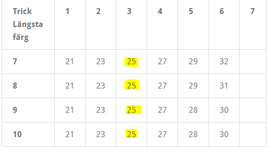
I tabellen till vänster visas HP-gränserna för olika BL om sannolikheten att kontraktet med DD-spel går hem överstiger 50%. Rekommendationen blir för att bjuda 4 i HF ska man förfoga 26hp med 7-kort trumf med en reducering med 2hp för varje extra trumf.
Rekommendationen för 3NT är 25hp oberoende av hur lång den längsta färgen är.
I tabellen till höger visas då “verkligheten”, dvs för vilka HP-gränser gäller att utfallet är över 50%. Vi ser då att för 4HF gäller 23,19 respektive 15hp beroende på trumflängden och att aldrig bjuda 4HF med 7 trumf. Orsaken till att gränserna är lägre i den högra tabellen är att det krävs att kontraktet blivit bjudit och att i denna uppställning även hänsyn tas till offringsmöjligheten med en lång trumf. Vi ser dock att för 8-korts trumf är rekommendationerna likvärdiga 23/24. Den övre gränsen i den högra tabellen återspeglar att med fler HP ska man satsa på slam då utfallet i MP riskerar minska då motståndarna har bjudit slam i det läget. Man ser också i den högra tabellen att 5LF i partävling är bara lönsamt om man har en 10-korts trumf och 23-26HP.
När det gäller 3NT får vi 24HP som gräns om längsta färgen är 7-8 kort, vilket stämmer väl med den teoretiska rekommendationen. Något överraskande ser vi att med 9- och 10-korts färg kan man prova 3NT med så lite som 22/20HP med framgång! Den teoretiska modellen (DD-analys) rekommenderar 25 oberoende av färglängd. Avvikelsen är spännande och mer detaljerad analys krävs av detta fenomen. En hypotes kan vara att i praktiskt spel mot 3NT baserat på långfärg är utspel och motspel så svårt att det sällan landar på DD-nivå utan att spelföraren får favörer i praktiskt spel som väl motiverar chansning på 3NT med en långfärg.
Vidare kan man i den högra tabellen utläsa hur högt man ska bjuda med 18-22HP, dvs i konkurrensläget. Rekommendationen från lagen, dvs 8->2, 9->3, 10->4 och 5 never verkar hålla bra! Verkligheten verkar till och med vara lite mer aggressiv då vi ser att 2HF med 7-kort trumf är lönsamt med 18-24HP. Man ser också att poänggränserna är högre och snävare i LF än i HF och att 4LF inte ska bjudas med mindre än 9-korts trumf och helst fler HP än motståndarna, med 10-korts färg kan man pruta lite på HP-gränsen.