I många böcker föreslås råd baserade på “lagen i bridge” när det gäller hur högt man ska bjuda i konkurrensbudgivning. Den enkla regeln är baserad på trumflängd med viss egen hänsyn till zon-förhållande utan några explicita råd om styrka, som antages var i närheten av 18-22 när man hamnar i konkurrens. Regeln är enkel 8/2, 9/3 och 10/4, dvs med 8-kortsfärg bjud på 2-trick, med 9 – 3 trick och med 10 – 4 trick. Hur framgångsrikt detta är i praktiken är ju beroende av hur aggressivt motståndarna bjuder och hur bra de spelar, men naturligtvis också på vilken styrka man gemensamt förfogar över.
Kan man då hitta en bättre vägledning på hur högt man ska bjuda om man vet exakt hur många hp och hur lång den gemensamma trumfen är. Det var lite av dessa tankegångar jag haft när jag dök in i siffrorna i databasen denna gång.
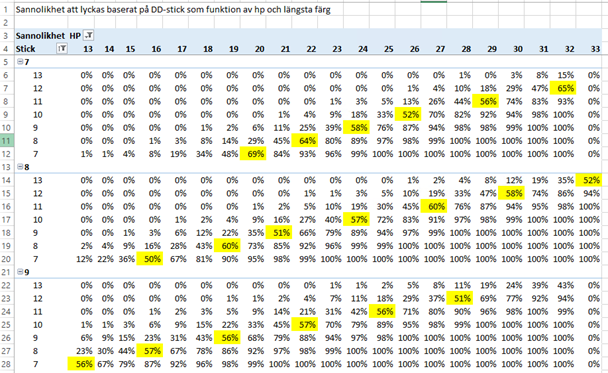
Efter en del pyssel lyckades jag få fram följande tabell:
Som vanligt mycket fler siffror än man kan memorera.. Det som visas är dels trumflängd 7,8 och 9. Inom trumflängd visar sedan tabellen hur många stick man har chansen att ta (sannolikheten) beroende den gemensamma styrka i hp. Allt är baserat på de c:a 100’ givar som finns i min databas, mao ett hyfsat underlag. Hur många stick man kan ta är baserat på vanlig DD-beräkning med dess fel och brister.
Vi kan hitta 69% i övre delen, vilket ska tolkas att det är 69% sannolikhet att lyckas spela hem 1 trick i färg (7 stick ) om man förfogar över 20hp tillsammans med en 7-korts trumf. Har man bara 19 är chansen 48%.
När det gäller utgång och slam hävdar de flesta böcker att chansen ska vara runt 50% för att bjudas, dessa punkter är utmärkta med gult i tabellen ovan.
Sammanställer man detta får man fram följande tabell som visar vilken nivå man ska bjuda som funktion av trumflängd och hp om man vill att chansen att lyckas ska var 50% eller bättre..
| Trumf/Trick | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 20 | 22 | 24 | 26 | 29 | 32 | |
| 8 | 16 | 19 | 21 | 24 | 27 | 30 | 33 |
| 9 | 13 | 16 | 19 | 22 | 25 | 28 | 33? |
| 10 | ? | 13 | 17 | 20 | 24 | 27 |
Inte helt överraskande verkar det behövas 3hp per stick.. Men det tycks också vara så att en hacka mer i trumf sänker kravet med 3hp, dvs det finns en stöld mer att ta, utom i höga kontrakt!
Motsvarande kan beräknas för NT-kontrakt och då får tabellen följande utseende:
| Trick Längsta färg |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 7 | 21 | 23 | 25 | 27 | 29 | 32 | |
| 8 | 21 | 23 | 25 | 27 | 29 | 31 | |
| 9 | 21 | 23 | 25 | 27 | 28 | 30 | |
| 10 | 21 | 23 | 25 | 27 | 28 | 30 |
Lite överraskande(?) tycks inte en långfärg påverka utfallet på samma sätt som för färgkontrakt, även om det finns möjlighet att få stick på hackor i långfärger i NT, möjligtvis lite på 5- och 6-tricks nivån. 25 hp gränsen för 3NT verkar vara giltigt oberoende av färglängd! Det verkar också som att 4HF alltid ger mer poäng än 3NT med samma styrka, utom med 7-korts trumf.
Om 50% ska användas som gräns när det gäller delkontrakt är inget som diskuteras i några böcker, så den gränsen är godtyckligt vald i tabellen ovan. Siffrorna med ? anger viss osäkerhet då bara rutor med mer än 100 observation är medtagna i underlaget.
Vill du själv titta lite på underlaget i Excel? Det finns här.
Slutsatser.
Att följa rekommendationen 8/2, 9/3 och 10/4 tycks ge 50% chans till att spela hem färg-kontrakt med 19-20hp, dvs om det blir bet så sitter korten snett och borde innebära i de flesta fall att motståndarnas kontrakt går hem. Undantag är sned trumfsits som ju bara drabbar de som spelar kontraktet i den färgen. Dvs tumregeln max 1 odubblad bet i zon och 2 i ozon är ofta bättre än att låta motståndarna spela sitt delkontrakt.
De gamla reglerna med att NT oftast är bättre än trumfkontrakt med 7-korts färg, dock krävs kanske en separation här för att se om 5-2 trumf är bättre än att bjuda NT. Dock bör man kanske ibland föredra 1NT (vid 8-korts trumf) som ju ger lika mycket som 2LF, dvs man ska oftast vara nöjd om man får spela 1NT i jämna lägen. Sedan konstaterar vi att 4HF ska väljas med 8+-trumf i de flesta lägen.